Welcome to
Topdach Limted
We are the leading provider of Voice over Internet Protocol (VoIP) services, wholesale minutes buying and selling, home appliances, and electronic vaping products.
We are committed to delivering the most reliable and innovative VoIP services and products to our customers, along with unbeatable customer service. With our easy-to-use and affordable VoIP solutions, you can make and receive calls on your home phone, computer, mobile device, or other VoIP-enabled device. Our wholesale minutes buying and selling services make it easy to save money while making domestic and international calls.
Our expansive selection of home appliances and electronic vaping products offer quality and convenience, with the latest and greatest technologies. With unbeatable prices and unbeatable customer service.
Topdach Limited is your one-stop shop for all of your VoIP, wholesale minutes, home appliances and electronic vaping needs. Thank you for choosing Topdach Limited, and we look forward to serving you!
A better way to talk business
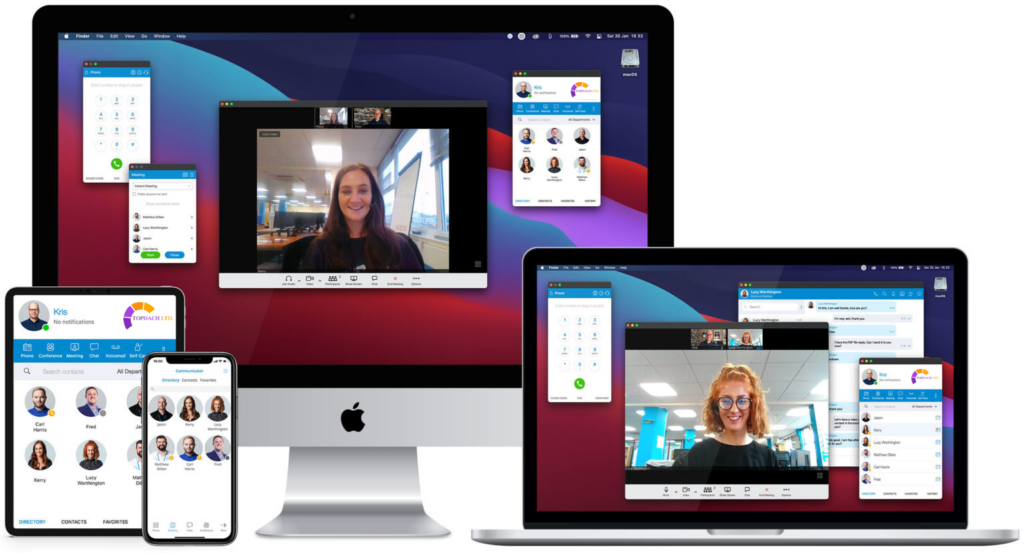
Topdach Limited, the complete communications platform for your business. Our platform can be used from any web browser to chat, call, video conference, share screens, and send files with your colleagues and customers. We offer a fully integrated service that can be used with a desk phone, softphone on your computer or laptop, or a mobile app on your smartphone or smartwatch. This eliminates any unnecessary upfront costs or hardware changes.
Topdach Limited, Communications
Our platform is easy to use, reliable, and secure – so you know that your conversations and data are safe. With our integrated communication platform, you can make and receive calls, share files, work collaboratively on projects, and more – all with the click of a button. Whether you’re a small business or a large enterprise, Topdach Limited has the tools you need to keep your business running smoothly.
Thank you for choosing Topdach Limited, and we look forward to helping you take your business to the next level.
End-to-end
Broadest suite of native apps. One unified platform. One user experience.
Adaptable
Flexible for your business. “Clicks not Code” admin. Front line empowerment.
Intuitive
Fast implementation. Modern user interface. No agent learning curve.
AI-infused
Intelligent engagements. Operational efficiency.
Adaptable
Flexible for your business. “Clicks not Code” admin. Front line empowerment.
Intuitive
Fast implementation. Modern user interface. No agent learning curve.
The most recommended cloud VoIP system

Topdach Limited, the leading provider of VoIP services. Our customer-first mentality has led us to achieve exceptionally high customer satisfaction ratings, and we take pride in providing services that go above and beyond our customers’ expectations. Our VoIP services are designed to be easy to use, reliable, and secure, so you can rest assured knowing that your conversations and data are safe. With our VoIP services, you can make and receive calls, share files, and collaborate with colleagues – all with the click of a button. We also offer exceptional customer service, so you can get the help you need quickly and easily. Thank you for choosing Topdach Limited.
Topdach Limited, keeps employees flexible and
productive with smart cloud calling.
Collaboration made easy
Topdach Limited, Hardware



Get In Touch

+44-8458600867
Info@topdach.uk
Unit 2, 18 Wintersells Road, West Byfleet, England, KT147LF
